20. 使用 Python 实现矩阵
向量 vs. 矩阵
向量是卡尔曼滤波器方程的一部分。但是你还需要学会使用矩阵。
你已经看过了 Python 如何在列表中代表向量。一个向量可以被视作简单的网格,其中每个分量都有一行和一列。如果你将向量视作网格,向量 \begin{bmatrix}17, 25, 6, 2\end{bmatrix} 将被这样表示:
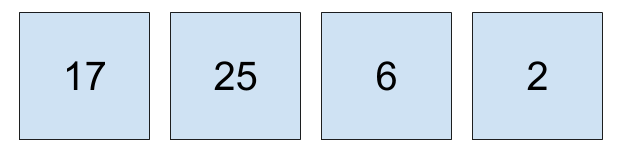
不过你也可以将这个向量称为矩阵。这四个向量分量是一个一行四列的矩阵,或者 1x4,其中 1 代表行的数量,4 代表列的数量。
但如果你将这个向量旋转一下,让它看起来像这样呢?
\begin{bmatrix}17 \\ 25 \\ 6 \\ 2 \end{bmatrix}
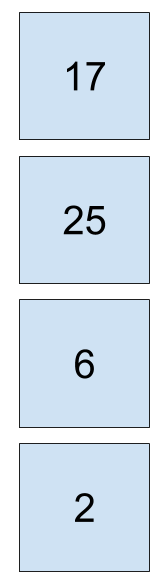
旋转向量
SOLUTION:
是作为矩阵的向量
SOLUTION:
4 行,1 列两个向量
如果你将一个向量像下面这样进行复制会发生什么?
\begin{bmatrix}17 &17 \\ 25 & 25 \\ 6 & 6 \\ 2 & 2\end{bmatrix}

现在你有了一个四行二列的 4x2 矩阵。将这个向量进行水平复制怎么样?
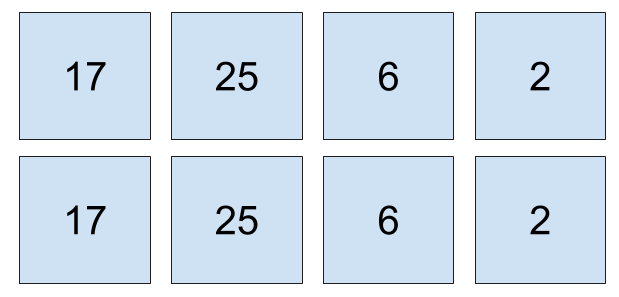
矩阵尺寸
SOLUTION:
2x4在 Python 中表示矩阵
因此,矩阵是一个 m 行 n 列的二维网格。看看下面这个矩阵,它的尺寸比之前例子中出现的矩阵都要大一些。
\begin{bmatrix}17 & 25 & 6 & 2 & 16 \\ 6 & 1 & 8 & 4 & 22 \\17 & 8 & 54 & 15 & 65 \\11 & 25 & 68 & 9 & 2\end{bmatrix}

这个矩阵是 4x5,它有 4 行 5 列。
你如何在 Python 中表示一个这样的矩阵?从最上面一行 \begin{bmatrix}17, 25, 6, 2, 16\end{bmatrix} 开始。当单独看最上面这行时,它看上去像一个向量。而在 Python 中,你使用列表来表示向量。
在 Python 中表示矩阵时,你可以将每一行视作 一个向量 :
first_row = [17, 25, 6, 2, 16]那么第二行呢?
second_row = [6, 1, 8, 4, 22]继续:
third_row = [17, 8, 54, 15, 65]
fourth_row = [11, 25, 68, 9, 2]矩阵访问
SOLUTION:
68使用一个变量来表示所有行
在之前,矩阵的每一行你都使用单独的变量来表示。接下来,我们将使用一个变量来表示整个矩阵。
如果你将每一行排列开来,你会得到一个列表组成的列表:
matrix = [first_row, second_row, third_row, fourth_row]如果你这样编写,矩阵的特点将会更加明显:
matrix = [
first_row,
second_row,
third_row,
fourth_row
]使用向量来代替这些变量,你将得到一长串列表组成的列表:
matrix = [[17, 25, 6, 2, 16],
[6, 1, 8, 4, 22],
[17, 8, 54, 15, 65],
[11, 25, 68, 9, 2]]或者,我们稍微简洁一点:
matrix = [
[17, 25, 6, 2, 16],
[6, 1, 8, 4, 22],
[17, 8, 54, 15, 65],
[11, 25, 68, 9, 2]
]像矩阵那样编写向量
SOLUTION:
x = [[1, 5, 9, 3, 1]]练习编写矩阵代码
在本节课的下一部分,你将会练习在 Python 中编写矩阵代码。